INSTRUMENTACIÓN ELECTRÓNICA
Introducción
Instrumentación Electrónica, Es la rama de la electrónica que se encarga del diseño y manejo de los aparatos electrónicos, sobre todo para su uso en mediciones.
Las mediciones de precisión de los valores de los componentes se realizan mediante uso de los puentes. Dependiendo del tipo de componente y de las características del mismo las mediciones se efectúan con el uso de un puente en particular.
En esta entrada daremos explicación de circuitos específicos como lo son los puentes de medición.
Puentes de Medición
Básicamente un puente de medición es una configuración circuital que permite medir resistencias en forma indirecta, a través de un detector de cero.
Existen puentes de continua y alterna.
Puentes en CC
Tienen el propósito de medir resistencias, de valores desconocidos, utilizando patrones que sirven para ajustar a cero (equilibrio del puente).
La configuración puente consiste en tres mallas. Se disponen de cuatro resistencias,entre ellas la desconocida, de una fuente de corriente continua y su resistencia interna, y un galvanómetro. Se estudiará la influencia de la sensibilidad del galvanómetro y de la limitación de la intensidad de corriente en los brazos del puente, así como la exactitud del puente con respecto al valor de la incógnita a medir.
Existen algunas variantes para medir resistencias muy altas o muy bajas.
Puente de Wheatstone
El puente de Wheatstone tiene cuatro ramas resistivas, una fuente de f.e.m (una batería) y un detector de cero (el galvanómetro). Para determinar la incógnita, el puente debe estar balanceado y ello se logra haciendo que el galvanómetro mida 0 V, de forma que no haya paso de corriente por él. Debido a esto se cumple que:
I1R1 = I2R2
Al lograr el equilibrio, la corriente del galvanómetro es 0, entonces:
I1 = I3 = E / (R1 + R3)
I2 = I4 = E / (R2 + Rx)
Donde Rx es R4, se obtiene:
R1 / (R1 + R3) = R2 / (R2 + RX)
Resolviendo:
R1.RX = R2.R3
Expresando Rx en términos de las resistencias restantes:
RX = R3.R2 / R1
R3 se denomina Rama Patrón y R2 y R1 Ramas de Relación.
El puente de Wheatstone se emplea en mediciones de precisión de resistencias desde
1• hasta varios M•.
Ejemplo:
Si R1 y R2 = 1 KΩ (Kilohmio) y R3 = 5 KΩ, Rx deberá de 5 KΩ para lograr que el voltaje entre A y B (VAB) sea cero (corriente igual a cero)
Así, basta conectar una resistencia desconocida (Rx) y empezar a variar R3 hasta que la corriente entre A y B sea cero. Cuando esto suceda, el valor de RX será igual al valor de R3
Una aplicación muy interesante del puente Wheatstone en la industria es como sensor de temperatura, presión, etc. (dispositivos que varían el valor de sus resistencias de acuerdo a la variación de las variables antes mencionadas).
Es en el amperímetro donde se ve el nivel o grado de desbalance o diferencia que hay entre el valor normal a medir y la medida real.
También se utiliza en los sistemas de distribución de energía eléctrica donde se lo utiliza para detectar roturas o fallas en las líneas de distribución
Puente de Thompson (Kelvin)
El puente Kelvin es una modificación del puente Wheatstone y proporciona un incremento en la exactitud de las resistencias de valor por debajo de 1• (ohm).
En donde RY representa la resistencia del alambre de conexión de R3 a Rx. El Galvanómetro se puede conectar al punto m o al punto n.
Cuando se conecta al punto m: RY se suma a Rx.
Cuando se conecta al punto n: RY se suma a R3.
Si se conecta el galvanómetro a p, la razón de la resistencia de n a p y de m a p iguala la razón de las resistencias de R1 y R2.
Rnp / Rmp = R2 / R1
La ecuación de equilibrio para el puente da:
Rx + Rnp= (R2 / R1)(R3 + Rmp)
A partir de las dos últimas ecuaciones Rx nos da:
Rx = R3.R1 / R2
Puente doble de Kelvin
El término doble se debe a que el circuito tiene un segundo juego de ramas de relación. Se utiliza para medir resistencias menores a 1[Ω].
Las resistencias Rx y Rp (resistencias desconocido y patrón respectivamente), son resistencias de cuatro terminales, construcción que se emplea para Shunt y patrones de resistencias.
La resistencia de cuatro terminales tiene dos pares de bornes, es decir dos bornes de tensión (bornes superiores) y dos bornes de corriente (bornes inferiores).
El equilibrio se cumple:
I1 = I2 ; I3 = I4 ; Ix = Ip
I1.R1 = Ix.Rx + I3.R3
I2.R2 = Ip.Rp + I4.R4
Resolviendo estas ecuaciones obtenemos:
RX = (R1 / R2).RP + (I3 / Ix).R1.[(R1 / R2) - (R3 / R4)]
Haciendo:
(R1 / R2) = (R3 / R4)
La expresión para Rx nos queda:
Rx = Rp.(R1 / R2)
Acoplando en forma mecánica a con R1 y b con R2, se logra medir resistencias desde 1• hasta aproximadamente 10μ• (Ohm).
Puentes en CA
Los puentes de corriente alterna son más versátiles y en consecuencia tienen más aplicaciones que los puentes de C.C. Se usan en medidas de resistencias en C.A., inductancia, capacidad e inductancia mutua, en función de patrones conocidos y relaciones conocidas de elementos.
Su forma básica consiste en un puente de cuatro ramas, una fuente de excitación (alterna) y un detector de cero (audífono, amplificador de C.A. con osciloscopio, etc.). Para bajas frecuencias se puede utilizar la línea de potencia como fuente de excitación; y a altas frecuencias se puede utilizar un oscilador.
La forma general de un puente de C.A. se presenta en
El equilibrio se alcanza cuando la respuesta del detector es cero o indica corriente nula.
La condición de equilibrio se logra de igual forma que en el caso de los puentes de continua, con la diferencia de que en las ramas en vez de resistencias tenemos impedancias, las cuales tendrán un modulo y una fase.
En condición de equilibrio tenemos:
EBA = EBC ó Z1.Z4 = Z2.Z3
De donde podemos ver que los productos de las impedancias serán iguales si se cumplen las siguientes dos condiciones:
|Z1||Z4|=|Z2||Z3|
(los productos de las ramas de los módulos opuestos deben ser iguales.)
θ1 + θ4 = θ3 + θ2
(la suma de los ángulos de fase de las ramas opuestas deben ser iguales.)
Cuando utilizamos notación compleja (Z= R + jB), la condición de equilibrio se logra cuando se cumple las siguientes condiciones simultáneamente:
La parte real del primer producto es igual a la parte real de segundo producto
La parte imaginaria del primer producto es igual a la parte imaginaria del segundo producto.
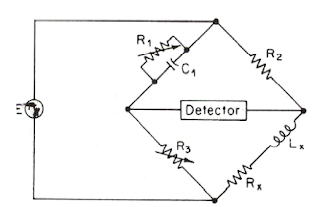
Puente de Maxwell
Este puente de C.A. se utiliza para medir una inductancia desconocida en términos de una capacitancia conocida. Una de las ramas de relación tiene una resistencia y una capacidad en paralelo
Escribiendo la ecuación en términos de Zx (impedancia de la rama desconocida). se obtiene:
Zx = Z2.Z3 / Z1
Utilizando la admitancia, donde w es la frecuencia angular (2.pi.f). Sustituyendo estos valores da:
Zx = Rx + jwLx = R2.R3 ( 1/R1 + jwC1)
Cuya parte real es:
Rx = R2R3 / R1
Y la imaginaria:
Lx = R2.R3.C1
Cabe aclarar que las resistencias se expresan en ohms, las inductancias en henrys y las capacitancias en faradios.
Puente de Hay
Como primera característica de este puente, se puede mencionar su utilización para la medición de inductancias. En la figura 7.13 se observa la configuración clásica del puente Hay. A primera vista este puente no difiere demasiado de su equivalente de Maxwell, salvo que en esta ocasión el capacitor C1 se conecta en serie con la resistencia R1, por lo tanto para ángulos de fase grandes la resistencia R1 debe tener un valor muy bajo. Es esta pequeña diferencia constructiva la que permite su utilización para la medición de bobinas de Q alto (Q>10).
Separando términos reales e imaginarios, y como en ambas ecuaciones están presentes los términos Lx y Rx, se
deben resolver simultáneamente, entonces:
También se puede reemplazar en la ultima ecuación 1 / (Q^2) = (W^2)(C1^2)(R1^2)
Para Q>10, el término (1/Q2)<1/100, por lo tanto:
Lx = R2R3C1 (Casi igual)
En resumen se puede decir que para la medición de inductores con Q alto (Q>10) se debe utilizar el puente Hay. En el caso de inductores de Q bajo (Q<10) el método apropiado es la medición a través del puente Maxwell.
Puente de Owen
El puente Owen es ampliamente utilizado para la medición de inductores, más precisamente para aquellas inductancias con factor de calidad bajos (Q<1). Su configuración clásica se representa en la figura, y observando esta se puede remplazar la ecuación de equilibrio para los puentes de C.A.:
Z1.Z3 = Z2.Z4
Rx = C1.R2 / C3 Lx = C1.R2.R3
Como se puede ver de las ecuaciones, el equilibrio del puente es independiente de la frecuencia, y como el término C1.R2 es conocido, dicho equilibrio depende exclusivamente de los elementos ajustables C3 y R3.
Puente de Schering
El puente de Schering se utiliza para la medición de capacitores, siendo de suma utilidad para la medición de algunas de las propiedades de aislamiento (tgd) , con ángulos de fase muy cercanos a 90°.
En la figura, se muestra el circuito típico del puente Schering, nótese que la rama patrón (rama 3) solo contiene un capacitor. Por lo general, el capacitor patrón es de mica de alta calidad para las mediciones generales de capacidad, o puede ser de un capacitor de aire para mediciones de aislamiento.
Los capacitores de mica de buena calidad, poseen pérdidas muy bajas y por consiguiente un ángulo aproximado de 90°, en cambio un capacitor de aire tiene un valor muy estable y un campo eléctrico muy pequeño, por lo tanto el material aislante se puede conservar fuera de cualquier campo fuerte.
Puesto que el capacitor patrón está en la rama 3, las sumas de los ángulos de fase de las ramas 2 y 3 será 0° + 90° = 90°, para cumplir con la ecuación de equilibrio, se necesita que los ángulos de fase de las ramas 1 y 4 sea de 90°. La conexión en paralelo del capacitor C1 con el resistor R1 proporciona a la rama 1 un ángulo de fase pequeño, ya que en general la medición desconocida Zx posee un ángulo de fase menor de 90°.

Planteando la ecuación general de equilibrio de los puentes de CA.
Z1.Z4 = Z2.Z3
Igualando términos reales e imaginarios,
Rx = R2.C1 / C3
Cx = C3.R1 / R2
Si se observa en el circuito, se puede ver que las dos variables que se escogen para el ajuste del equilibrio son el capacitor C1 y el resistor R2.
El factor de potencia o cos j de la impedancia desconocida será:
PF = Rx / Zx
Y el aislamiento seria:
tgd = 1 / Q
ó
tgd = w.C1.R1
Si el resistor R1 tiene un valor fijo, el dial del capacitor C1 se puede calibrar directamente en función de la tgd. Esta es la utilidad práctica del puente de Schering, ya que el término w aparece en la expresión de la tgd por lo tanto la calibración del dial C1 solo se conserva para la frecuencia a la cual se calibró el dial. Se puede utilizar una frecuencia
diferente multiplicando el dial C1 por la relación de las dos frecuencias.
Puente de Wien Serie:
Este puente se utiliza para medir valores de capacitancia desconocidas, cuyo factor de pérdida “D” es bajo.
Puente de Wien Paralelo:
Este puente se utiliza para medir valores de capacitancia desconocidas, cuyo factor de pérdida “D” es alto.
Bibliografia
1) 'Instrumentación Electrónica Moderna y Técnicas de Medición' de W. Cooper. Editorial Prentice Hall 1982.
2) 'Análisis de medidas eléctricas' de E. Frank, Editorial Mc Graw Hill 1969
 |
| ANEXO. Símbolos Básicos en la Instrumentación generalizada. |